NETWORKS
2024
1) Students have to draw the interconnecting lines between nodes or locations.
2) For Excellence, application of the Kruskal algorithm used to justify the minimum and maximum spanning tree will be sufficient.
The three aspects of Networks we will be investigating are
1) Traversability
2) Shortest Path
3) Minimum Spanning Tree (or maximum)
1) Traversability
2) Shortest Path
3) Minimum Spanning Tree (or maximum)
NAMING THE PARTS OF THE NETWORK
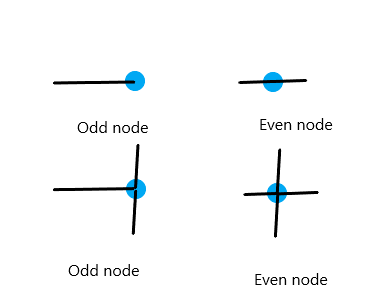
Nodes are connected by edges, also known as arcs, paths, trails etc. Think of the nodes as towns on a map and the roads (paths) connecting them, edges. Nodes are either odd or even depending on the number of paths or edges entering or leaving a node.
TRAVERSABILITY- this is really important
A traversable network is one that can be drawn without lifting the pen from the paper and without retracing the same path (arc). The rules that make a network traversable are:
- if all nodes are even order, we can start anywhere (and finish anywhere including back at the start node which is called an Euler circuit)
- if there are EXACTLY two nodes with an odd order (all others even), we must start at one odd node (and finish at the other odd node). This is called an Euler path.
SHORTEST PATH
Shortest path is the shortest route between two nodes.
MINIMUM SPANNING TREE
Minimum Spanning Trees are used in designing fibre optic networks and water supply distributions in cities. Several mathematical methods exist for finding minimum spanning trees, including Prim's and Kruskal's algorithms (not Krusty the clown!)
NETWORKS ACTIVITY 1
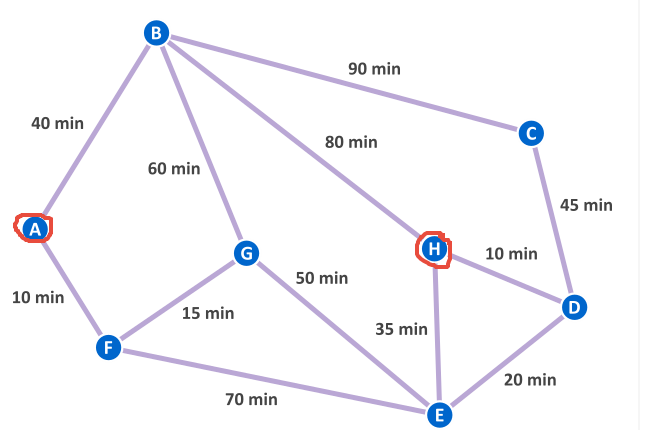
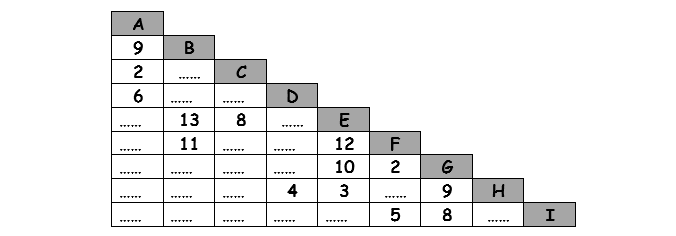
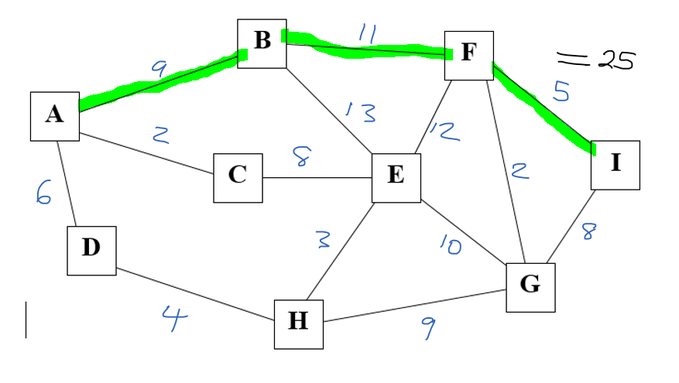
1) Find the shortest path between nodes A and I. State the order of nodes chosen. You can draw a tree diagram or trial and error is OK for this standard.
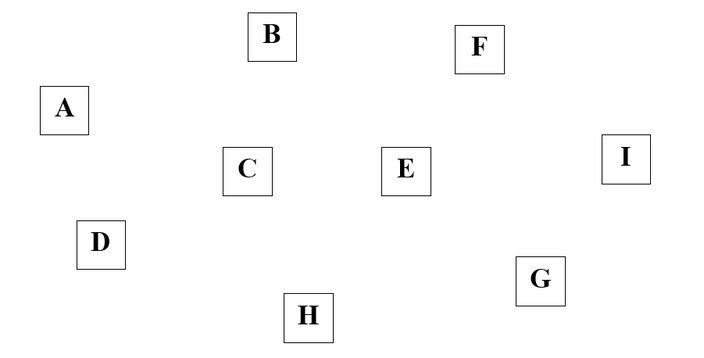
students need to connect the nodes together
from a blank map or diagram
merit excellence requires use of
Dijkstra's algorithm
You need to list the nodes as well as the answer for the shortest path. A - B - F - I = 25 If there is a unit in use then use the unit eg in this example the unit of measurement is in 1000's of km so the answer would be 25000 km. (yes I know the distances appear somewhat astronomical).
2) Can the whole of this set of paths be traveled going on each path once and only once? Give a full explanation for your answer.
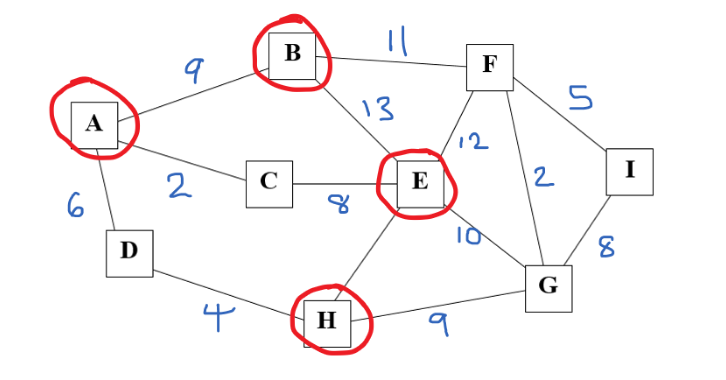
In other words is the path traversable? For this to be possible there needs to be no odd nodes (all even) or there are two odd nodes and the others even. Circle all the odd nodes above and you can see that there are 4 odd nodes which breaks the rules of traversability. So this network is not traversable.
3) What is the minimum spanning network for this and what is the distance of span required?
guessing and checking gets you Achieved
We will use Kruskal's Algorithm to solve this network problem and take it one step at a time. Firstly the number of paths we need is found from a simple formula which states
The number of paths = number of nodes - 1
= 9 -1
= 8
This doesn't tell us the answer exactly but it puts a limit on what our answer could be. If you have more than or less than this number of pathways the answer is incorrect. Now write out 8 spaces where we will in turn allocate each path starting from the smallest distance to the largest distance. If one pathway creates a circuit, remove it, (that might take a little time to understand).
The number of paths = number of nodes - 1
= 9 -1
= 8
This doesn't tell us the answer exactly but it puts a limit on what our answer could be. If you have more than or less than this number of pathways the answer is incorrect. Now write out 8 spaces where we will in turn allocate each path starting from the smallest distance to the largest distance. If one pathway creates a circuit, remove it, (that might take a little time to understand).
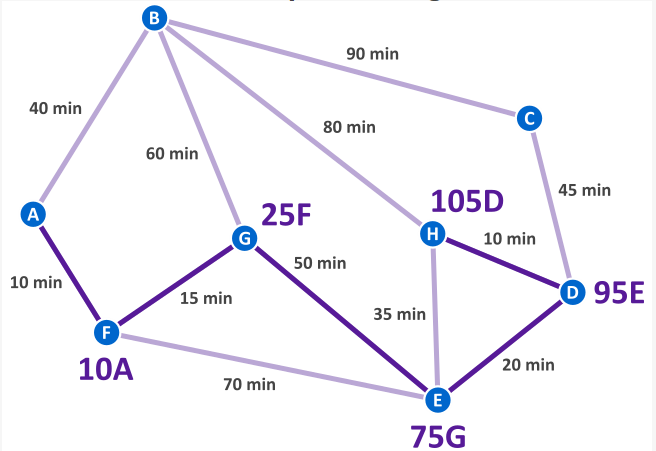
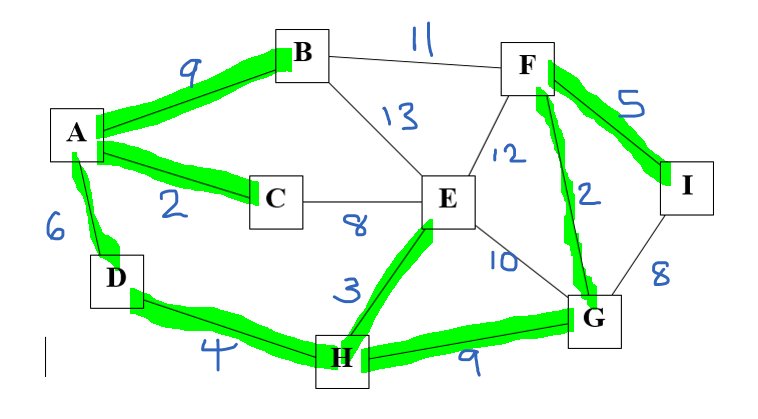
AC FG EH DH FI AD CE GI HG AB
2 2 3 4 5 6 8 8 9 9
2 2 3 4 5 6 8 8 9 9
There should only be 8 pathways in use (out of the 14 available) so the paths which cannot be used (indicated in red). Because CE and GI create a circuit we can eliminate both of those paths. It makes sense to remove the largest paths because we want a minimum distance to span. So don't include both 8's.
If we now add up the 8 paths we get 40, so the answer is 40000 km for the minimum spanning tree.
If we now add up the 8 paths we get 40, so the answer is 40000 km for the minimum spanning tree.
How this will look in your assessment.
"Looking at my highlighted network and using Kruskal's algorithm, I found the least distance that connects all 9 locations is 40,000 km".
"Looking at my highlighted network and using Kruskal's algorithm, I found the least distance that connects all 9 locations is 40,000 km".
4) What is the maximum spanning network for this and what is the distance span required?
We follow the same process as before for finding the minimum spanning network or tree. This time we begin by selecting the largest spans first. Again we have 8 nodes as before.
The number of paths = number of nodes - 1
= 9 - 1
= 8
Justification
With 9 nodes there will be 8 pathways connecting all 9 nodes together.
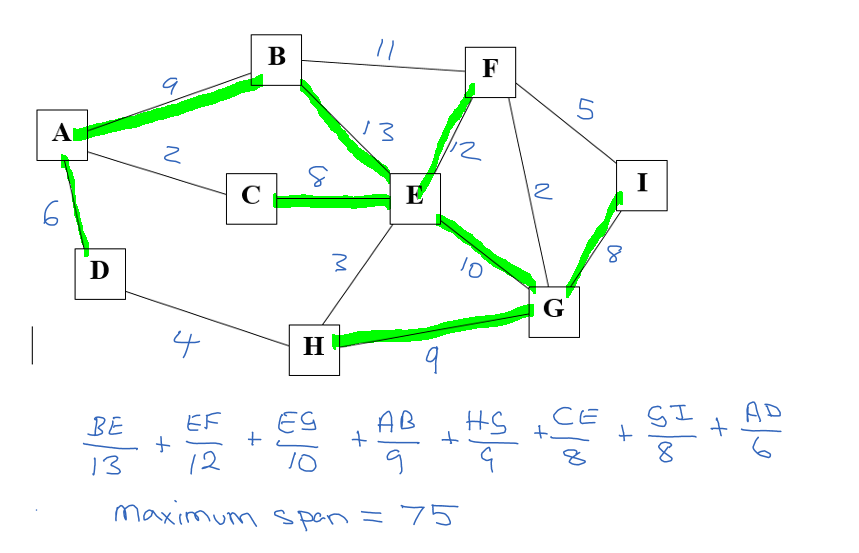
Start with the largest values which are 13 and 12 connecting B to E and E to F respectively. But connecting B to F would form a circuit which is not permitted. The next largest value is 10 connecting E to G. There are two paths with the same value of 9 connecting A and B, and again connecting H and G. and they can both be added to the network path. C to E and G to I have the same value of 8 and both can be accepted as no circuits are formed with their addition. Finally the eighth path has a value of 6 and connects A to D. This completes the spanning tree.
With 9 nodes there will be 8 pathways connecting all 9 nodes together.
Start with the largest values which are 13 and 12 connecting B to E and E to F respectively. But connecting B to F would form a circuit which is not permitted. The next largest value is 10 connecting E to G. There are two paths with the same value of 9 connecting A and B, and again connecting H and G. and they can both be added to the network path. C to E and G to I have the same value of 8 and both can be accepted as no circuits are formed with their addition. Finally the eighth path has a value of 6 and connects A to D. This completes the spanning tree.
You may notice that the path BF which has a distance value of 11 has been ignored because it doesn't improve the connectivity (law - no loops permitted in the network) so it becomes redundant. So the maximum span is 75,000 km.
"Looking at my highlighted network and using Kruskal's algorithm, I found the maximum distance that connects all 9 locations is 75,000 km".
"Looking at my highlighted network and using Kruskal's algorithm, I found the maximum distance that connects all 9 locations is 75,000 km".